Performance Analysis of Sorting Algorithms: part 2 of 2

4.0 Results and Analysis

4.1 Timing Results

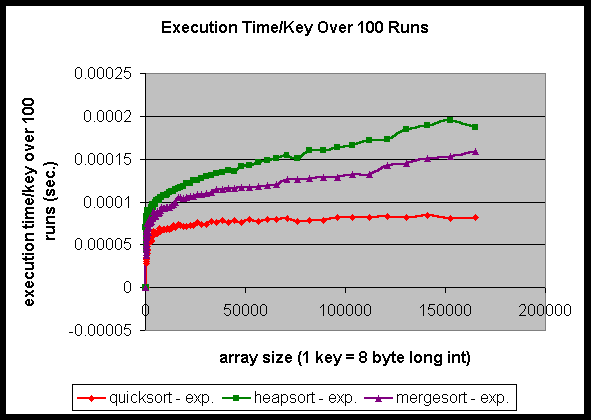
Figure 1: Performance of the sorting programs in terms of speed.

Figure 1 shows the timing results for all three sorting programs in terms of the execution time per key, where a key is an element in the sorting array. Quicksort is the fastest, then mergesort, and finally heapsort. The sorting array size covers from 100 keys to 164876 keys. This spans a set of sorting keys from one that all fits into the level one cache to one that does not fit into the level three cache. We are sorting long integers in C which are each eight bytes long. In looking at this graph, we noticed two ways that cache might be affecting the performance. First, the ranking of these three sorting programs could in some way be affected by cache. Since all three algorithms have complexity O(N log N), is it possible that the cache is doing something here that makes their performance ranking this way? Second, each timing curve extends smoothly as the array size increases. But is there a possibility that the cache is affecting the curve in some way here? To further investigate these two possibilities, we instrumented the following experiments. In order to find out these answers, we first need to determine the sorting algorithm’s rankings based on the theoretical complexity analysis. To do this, the next experiment we performed is the instruction count for the three sorting programs.

4.2 Instruction Count

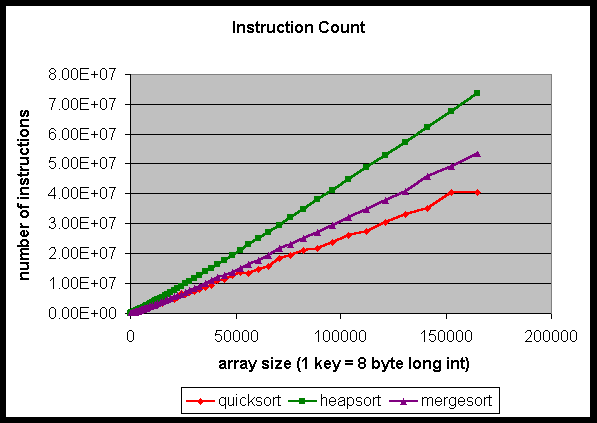
Figure 2: Instruction count of the sorting programs.

Figure 2 shows the instruction count in sorting the array as the array size increases. For all the array sizes, quicksort executed the fewest instructions, then mergesort, then heapsort. Because the number of instructions executed is the same whether running on a cached or non-cached architecture, the ranking determined by the instruction count should be the same as if assuming the cache has no affect on the overall performance. Since the theoretical analysis is based on a non-cached architecture, an analysis simply focusing on the program’s instruction count will give a ranking in accordance to the theoretical complexity. As seen from Figures 1 and 2, the theoretical ranking is the same as the experimental ranking. Therefore, there is no proof yet that cache is affecting the performance of the sorting algorithms. Even if cache did affect the ranking, the effect is not significant enough as to change the order of the ranking.

Since cache does not make any significant impact on the algorithm’s ranking, we next determined if cache affects the performance curve trend for each sorting program. In looking at Figure 1, we see that each curve extends smoothly, and there is no significant drop in execution time around any of the cache sizes. Therefore, in order to determine if cache affects the performance of the sorting algorithms, we plotted the theoretical execution time equations. Figure 3 shows the results.

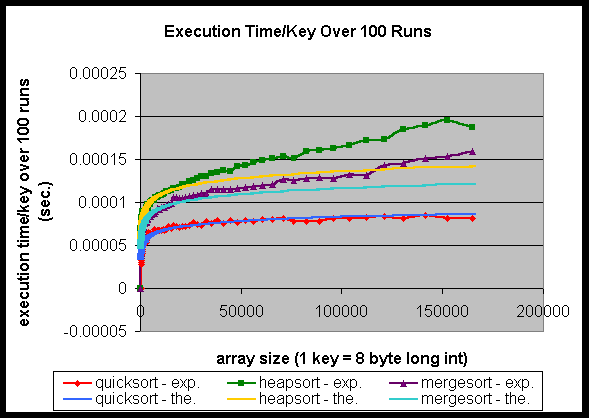
Figure 3: Comparison of the experimental timing results with the corresponding theoretical execution time equations.

For quicksort, the equation corresponding to the theoretical curve is
Y = (C1N ln N + C2ln N + C3N + C4)/N eq. 1

where C1 = 7.2 x 10-6. C2, C3, and C4 are not given because the last three terms do not make any significant changes to the theoretical curve.

This is derived from the following equation
T(N) <= 2(N + 1)(ln N + g - 1.5) + 0(1)
where g = 0.577 = Euler's Constant. eq. 2

Equation 2 is found in reference http://wannabe.guru.org/alg/.

The equation corresponding to the theoretical curve for heapsort is
Y = (C1N log N + C2 N + C3)/N eq. 3

where C1 = 8.2 x 10-6. Similarly, C2, and C3 are not given because the last two terms do not make any significant changes to the theoretical curve.

According to Donald Knuth, the average execution time for heapsort is based on an empirical estimate since the theory is incomplete. He has determined that the average execution time for heapsort is 23.08 N ln N + 0.2 N. Therefore, we have based our theoretical curve on his empirical results.

The equation corresponding to the theoretical curve for mergesort is
Y = (C1N log N + C2 N + C3)/N eq. 4

where C1 = 7.0 x 10-6. C2, and C3 are not given for the same reasons above.

This is derived from the following equation
T(N) = N log2N - N + 1 eq. 5

Equation 5 is found in reference http://wannabe.guru.org/alg/.

In the above equations, N is the sorting array size and T(N) is the total execution time.

Comparing the theoretical complexity curves with the experimental timing curves, we noticed that the two curves match very closely only for quicksort. For the other two programs, heapsort and mergesort, there is an obvious mismatch, starting when the array size is small. Therefore, in order to find out where those mismatches start, we zoomed in to the smaller array sizes in order to find out when the experimental timing results start to deviate from the theoretical execution time results. The result is shown in Figure 4.

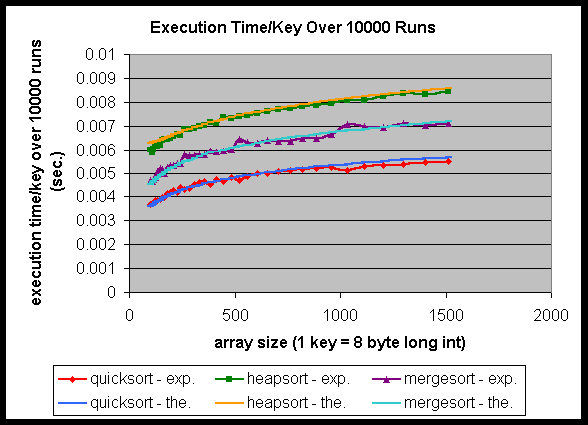
Figure 4: Experimental and theoretical performance below the level one cache size.

The theoretical curve equations in Figure 4 are the same as Equations 1, 3, and 4, except that the constants are different. For quicksort, C1 = 7.8 x 10-4, C2 = 1.0 x 10-3, C3 = 0, and C4 = -5.0 x 10-5. For heapsort, C1 = 8.25 x 10-4, C2 = -2.0 x 10-4, and C3 = 0.1. Finally, for mergesort, C1 = 6.8 x 10-4, C2 = 0, and C3 = 0.

From the zoomed results, it is seen that for heapsort and mergesort, the experimental timings start to deviate from the theoretical timings around the array size 1024, which corresponds to 8 kbytes of memory since we are sorting eight byte long integers. Since the level one cache size of the AlphaStation 500 is 8 kbytes, it means that the deviations start around the level one cache size. Something is happening around the level one cache size.

In order to understand the significance of this, let’s look at how the sorting programs work in terms of their cache performance on a system with a cached memory architecture. When the array size being sorted is smaller than the level one cache size, all of the elements of the array stay in the cache during the program’s entire execution. This makes the program execute as if there were no cache in the memory architecture at all. However, when the array size gets larger than the level one cache size, it does not fit in the level one cache anymore. All of the elements will not fit in the cache during the program’s entire execution, which will result in elements getting evicted due to capacity or conflict misses. Therefore, the cache will start to affect the performance of the programs when the array size is larger than the level one cache size, regardless of whether it is a single-leveled cache architecture or multi-leveled cache architecture.

This is what we saw in Figure 3. So it means that cache has an extra effect here. As further proof in Figure 4, when the array size becomes larger than the level one cache size, some elements will get evicted due to capacity or conflict misses, which results in the program speed suffering, and causes the deviation from the theoretical complexity curve.

So we see one way that a cached architecture does affect the performance of the sorting programs. Another feature we noticed in Figure 3 is that the degree of deviation for heapsort and mergesort are different. Heapsort showed a more serious deviation than mergesort. If the deviation is due to the cache, then we should also be able to explain the difference of the deviation degree by some measure of cache. We hypothesize that this is due to the difference in the cache miss rate. Therefore, we also ran Dinero cache simulations to simulate the cache performance of the three sorting programs.

4.3 Cache Miss Rate

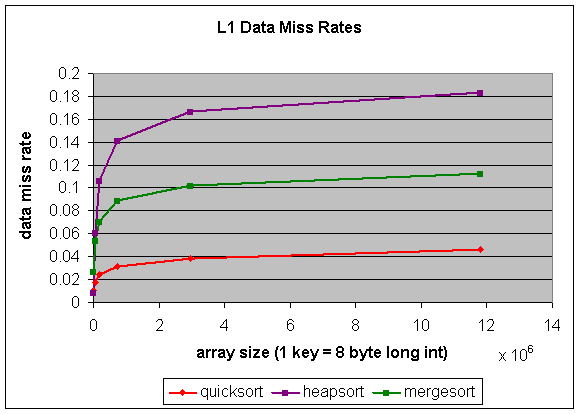
Figure 5: Data cache miss rates for the sorting programs.

We simulated only data load and store because by analyzing the three sorting programs, we know that the instructions needed will fit in the 8 kbyte level one instruction cache. So the performance of the instruction cache should not affect the overall performance of the sorting programs. In addition, not simulating the instruction cache will also save significant time and processing power. The data miss rates for the three sorting programs are shown in Figure 5. From the figure, it can be seen that quicksort has the lowest miss rate, then mergesort, followed by heapsort. Heapsort has higher data miss rates than mergesort, so the deviation for heapsort is greater than the deviation for mergesort. Therefore, we have two proofs that the cache does affect the performance of these sorting programs.

5.0 Summary and Conclusions

From current research, we know that cache does affect the performance of the sorting algorithms. In this paper, we showed how quicksort, heapsort, and mergesort are affected by cache. From the experimental results, it is seen that the performance ranking of the three sorting programs running on a system with a cached memory architecture is consistent to the ranking based on a non-cached architecture. However, when we compared the theoretical execution time equations, which is based on a non-cached memory architecture, with the experimental timing results, which is obtained by running in a system with a cached memory architecture, we noticed that there is a mismatch between the two curves that starts around the level one cache size. From this we deduced that a cached architecture does affect the performance of the sorting programs in comparison to a non-cached architecture. In order to find out what factor affects the difference in the degree of mismatch between the experimental timing curves and the theoretical performance curves for heapsort and mergesort, we ran Dinero cache simulations to obtain the data miss rates for the three sorting programs. From the simulation results we proved that higher data miss rates resulted in a higher deviation degree. This further proves that a cached architecture does affect the performance of the sorting programs in comparison to a non-cached architecture. From our experiments, we were able to determine in what way the cache affects the performance of the sorting algorithms, and how significant the effect is.

As seen from the analysis, cache does affect the performance of heapsort and mergesort, because their experimental timing curves deviates from the theoretical performance curves when the sorting array size becomes larger than the level one cache size. However, this effect caused by the cached architecture is not significant enough to change the performance ranking of the sorting programs based on a non-cached architecture. Finally, all of the above results clearly show that quicksort is really a cache friendly sorting algorithm. From Figure 3, we see that there is very little deviation between the experimental timing curve and the theoretical execution time equation for quicksort. Correspondingly in Figure 5, quicksort has a very low miss rate over all array sizes. The performance of quicksort is good not only due to its algorithm but also due to its good cache performance.

Our experimental work only investigated three sorting algorithms — quicksort, heapsort, and mergesort. Future work in this area includes studying other sorting algorithms among the numerous algorithms that have been developed over the years. In addition, since our experimental timings were only done on one machine, the Digital AlphaStation 500/400 MHz, future work will also include experimental timings on other machines. In short, as the increase in memory speed is not keeping up with the increase in processor speed, whether an application has a good memory performance will have a significant effect on its overall performance. As the memory - processor speed gap continues to widen, more and more importance will be given to memory performance. Therefore, in analyzing these sortng algorithms, it will become increasingly more important to analyze their cache performance as opposed to only analyzing their performance based on the theoretical complexity.

Tags: heapsort, mergesort, uicksort